손실함수 모음집

개요

• 다양한 형식의 Loss function들 모음집
• Loss function은 머신러닝의 핵심 개념이다. 이 함수를 최소화하는 방향으로 학습이 진행되어야 한다.

import seaborn as sns
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd

def MSE(pred_y, y):
    losses = []
    errors = []
    for i in range(len(pred_y)):
        losses.append(np.sum((pred_y[i] - y[i])**2)/len(pred_y))
        errors.append(np.sum((pred_y[i] - y[i]))/len(pred_y))
    return losses, errors

def RMSE(pred_y, y):
    losses = []
    errors = []
    for i in range(len(pred_y)):
        losses.append(np.sqrt(np.sum((pred_y[i] - y[i])**2)/len(pred_y)))
        errors.append(np.sum((pred_y[i] - y[i]))/len(pred_y))
    return losses, errors

def MAE(pred_y, y):
    losses = []
    errors = []
    for i in range(len(pred_y)):
        losses.append(np.sum(abs(pred_y[i] - y[i]))/len(pred_y))
        errors.append(np.sum((pred_y[i] - y[i]))/len(pred_y))
    return losses, errors

iris = load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)
model = LinearRegression()
model.fit(x_train, y_train)
pred_y = model.predict(x_test)

회귀모형

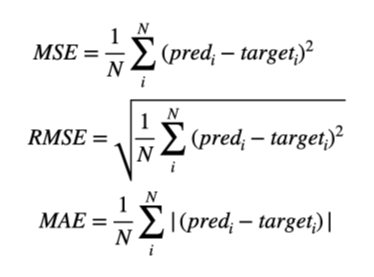
Mean Squared Error

• MSE: 예측값과 실재값의 차이를 제곱한 것의 평균을 구한 값이다.
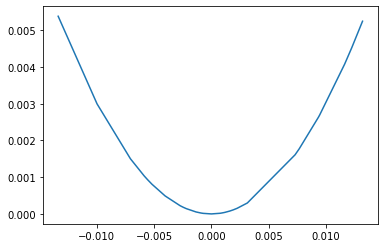
• 제곱을 하였기 때문에 항상 이차식의 형태로, 아래 그림과 같이 모든 구역에서 미분이 가능하다.
• 제곱을 하기 때문에 이상치에 대해 매우 민감하다.
• 아래의 그래프를 보면 알 수 있듯이, error가 커질수록 기하급수적으로 loss가 증가하는 것을 알 수 있다.
• 데이터의 신뢰도가 매우 클 때 이용 가능하다.

mse_losses, mse_errors = MSE(pred_y, y_test)

sns.lineplot(x = mse_errors, y = mse_losses)

<AxesSubplot:>

​

​

Root Mean Squared Error

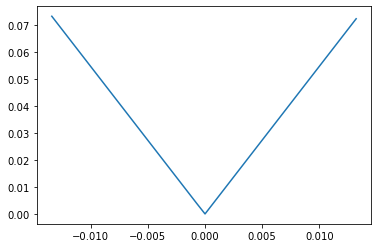
• RMSE는 MSE 전체에 루트를 씌우므로 MSE의 민감도를 낮춘 것이다.
• 민감도는 줄어드나, 아래의 그림과 같은 그래프를 가지므로 미분 불가능한 지점을 갖게 된다.

rmse_losses, rmse_errors = RMSE(pred_y, y_test)

sns.lineplot(x = rmse_errors, y = rmse_losses)

<AxesSubplot:>

​

​

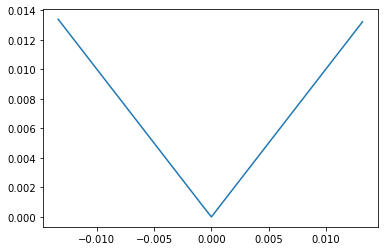
Mean Absolute Error

• MAE는 MSE의 제곱 대신 절댓값을 씌운 형태이다. 제곱이 들어가지 않으므로, error에 대하여 가장 Robust하다.

mae_losses, mae_errors = MAE(pred_y, y_test)

sns.lineplot(x = mae_errors, y = mae_losses)

<AxesSubplot:>

Logistic Regression에서 사용하는 Loss Function

• 변수가 Categorical일 때 다음과 같이 확률을 softmax 기법을 통해 모델링 할 수 있다.
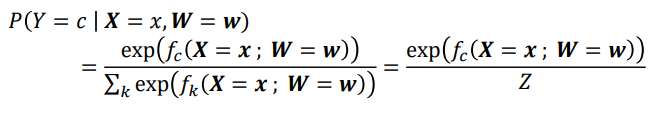
• X는 input variable, W는 각 변수에 대한 weight(가중치)이다.
• 거꾸로 회귀하여 w를 구하기 위해서 우린 D를 다음과 같이 설정할 것이다.
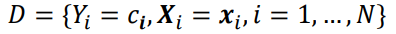
• D라는 조건에서 W가 w일 확률은 다음과 같다.
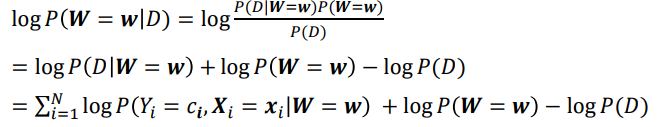
• 이때 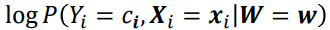는 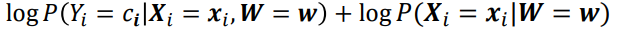로 분해할 수 있다.
• logP(W=w), logP(D), logP(X_i=x_i|W=w) 모두 상수이므로 우리는 다음과 같은 최적화 식을 구할 수 있다.
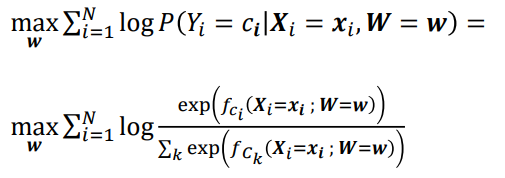
• 여기에 negative sign과 평균을 구하면 loss function 완성이다.

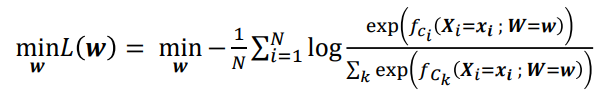
Cross-Entropy(Log Loss)

• 분류 모델 등에서 자주 사용하는 손실 함수이다. 각각의 데이터를 비교하기 보다, 데이터의 분포를 비교한다고 이해하는 것이 편하다.
• Entropy는 다음과 같이 구할 수 있다. (Log(p)는 p가 0과 1 사이의 값에서 음의 값을 가지므로 음의 기호를 붙인다.)
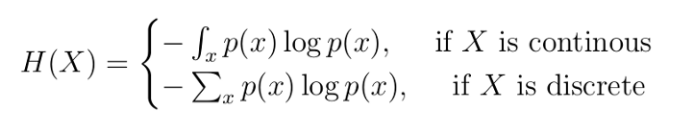
• 엔트로피는 불확실성을 나타내는 언어이다. 열역학에서 주로 쓰이는 용어인데, 각 계의 에너지가 균등할 수록 엔트로피가 높아진다고 한다. 이는 데이터 과학에서도 마찬가지로, 균등한 확률일 수록 엔트로피는 높아진다.
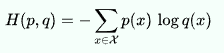
• 앞서 구했던 엔트로피와 달리, Cross-Entropy는 q라는 분포가 등장한다. 우리는 p분포를 Ground truth로 보고, q분포를 예측한 분포로 본다. 앞서 구한 Logistic regression의 loss function을 살펴보자.
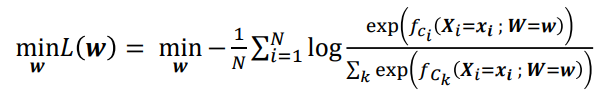
• 사실 Logistic regression는 cross-entropy의 p 분포에서 i번째 sample이 100%, 즉, (1,0,0,0)과 같을 때와 같은 형태를 띤다.
• Logistic regression의 loss function을 좀 더 general하게 바꾼 것이 Cross-Entropy라고 이해하면 좋을 것이다.

Entropy 예제

# 예측하기 어렵다는 것은, 확률이 균등하여 뽑기에 가깝다는 뜻.
print(f'p가 예측하기 쉬운 분포일 때 Entropy = {-(0.8*np.log(0.8) + 0.1*np.log(0.1) + 0.1*np.log(0.1))}')
print(f'p가 예측하기 어려운 분포일 때 Entropy = {-(0.3*np.log(0.3) + 0.3*np.log(0.3) + 0.4*np.log(0.4))}')

p가 예측하기 쉬운 분포일 때 Entropy = 0.639031859650177
p가 예측하기 어려운 분포일 때 Entropy = 1.0888999753452238

Cross-Entropy 예제

print(f'p와 q가 비슷한 분포일 때 Cross-Entropy = {-(0.8*np.log(0.7) + 0.1*np.log(0.2) + 0.1*np.log(0.1))}')
print(f'p와 q가 완전히 다른 분포일 때 Cross-Entropy = {-(0.8*np.log(0.3) + 0.1*np.log(0.5) + 0.1*np.log(0.2))}')

p와 q가 비슷한 분포일 때 Cross-Entropy = 0.6765422556938006
p와 q가 완전히 다른 분포일 때 Cross-Entropy = 1.1934367527601535

Cross-Entropy와 MSE의 비교

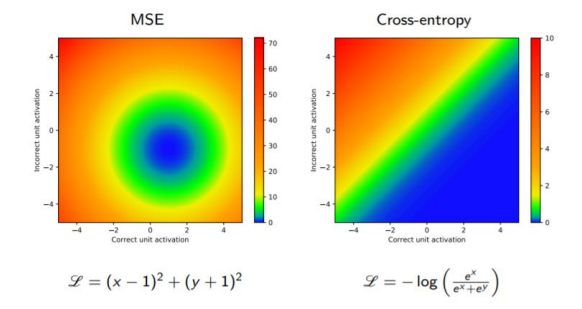
• MSE는 중심으로부터 얼마나 떨어져있는가에 따라서 loss를 구하기 때문에 분포의 비교에 적합하지 않다.

Kullback- Leibler Divergence

• KL-Divergence는 Probability Density Distribution 형태의 P(x)와 Q(x)의 차이를 구하는 방식으로 Cross-Entropy와 매우 유사하다.
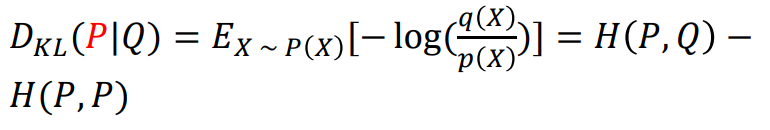
• Cross-Entropy - Entropy의 형태를 띤다.
• 사실, P는 ground truth distribution인 경우가 많으므로 H(P,P)는 상수이다. 즉, KL-divergence를 최소화하는 것은 Cross-Entropy를 최소화하는 것과 동일하다.
• KL-divergence는 거리 개념이 아니다. 아래의 예제와 같이 P와 Q의 위치를 바꾸었을 때 값이 다르다. 이는 Cross-Entropy도 마찬가지이다.

P = [9/25, 12/25, 4/25]
Q = [1/3, 1/3, 1/3]

KL_P_Q = 9/25*np.log((9/25)/(1/3)) + 12/25*np.log((12/25)/(1/3)) + 4/25*np.log((4/25)/(1/3))  
KL_Q_P = 1/3*np.log((1/3)/(9/25)) + 1/3*np.log((1/3)/(12/25)) + 1/3*np.log((1/3)/(4/25)) 

H_P_Q = -(9/25*np.log(1/3) + 12/25*np.log(1/3) + 4/25*np.log(1/3))
H_Q_P = -(1/3*np.log(9/25) + 1/3*np.log(12/25) + 1/3*np.log(4/25))

print(f'P가 ground truth일 때 KL-divergence는 {KL_P_Q}')
print(f'Q가 ground truth일 때 KL-divergence는 {KL_Q_P}')
print()
print(f'P가 ground truth일 때 Cross-Entropy는 {H_P_Q}')
print(f'Q가 ground truth일 때 Cross-Entropy는 {H_Q_P}')

P가 ground truth일 때 KL-divergence는 0.0852996013183706
Q가 ground truth일 때 KL-divergence는 0.09745500678538754

P가 ground truth일 때 Cross-Entropy는 1.0986122886681096
Q가 ground truth일 때 Cross-Entropy는 1.1960672954534974