Entropy-based Fuzzy SVM 구현하기
개요
- EFSVM은 imbalanced dataset을 분류할 때 유용하게 사용할 수 있는 머신러닝 기법이다.
- 일반적인 SVM 앞에 추가적인 장치를 적용해서 dataset 원본을 해치지 않고 imbalanced dataset을 handling할 수 있는 획기적인 방법이다.
- 파이선을 이용해서 EFSVM을 구현해보자.
EFSVM이란?
- SVM의 decision surface를 결정하는데 negative class의 영향력을 축소시키는 것을 목적으로 설계된 모형이다.
- 각 데이터의 중요도를 Entropy를 사용해서 나타낸다.
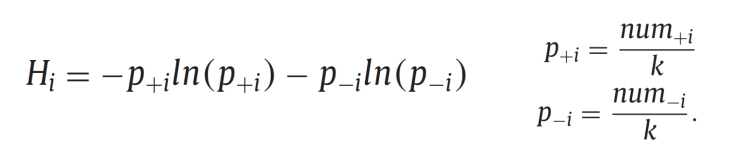
- K는 각 데이터의 Nearest Neighbor의 파라미터이다.
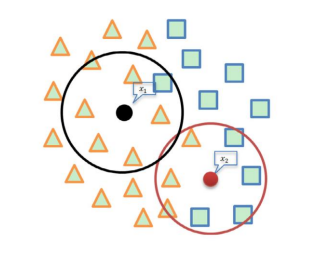
- K를 결정해서 KNN을 진행한 후, 그 내부에서 엔트로피를 계산한다.
- 샘플의 수가 적은 class를 positive, 많은 쪽을 negative라고 둔다. Negative class에 대해서만 엔트로피를 사용하여 중요도를 낮추어줄 것이다.
- 엔트로피 H의 최대, 최소를 구하고, 적절한 수의 Membership subset들을 만들어준다. 이때 Membership들의 엔트로피는 작은 것부터 큰 순서로 정렬해준다.
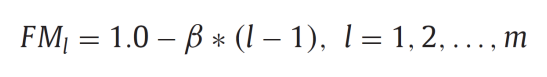
- 위 식과 같이 각 Fuzzy Membership별로 중요도를 낮춰준다. 이때 베타는 다음과 같은 지침을 갖는 하이퍼 파라미터이다.
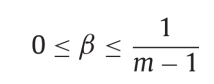
- 베타가 0에 가까울수록 Positive와 Negative class의 중요도에 대한 차별성이 떨어진다.
-
모든 데이터에 적용하면 다음과 같은 결과를 얻을 수 있다.
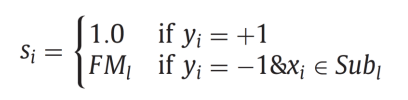
- 다음 식을 보면 우리가 구한 s가 어떤 역할을 하는지 바로 알 수 있다.
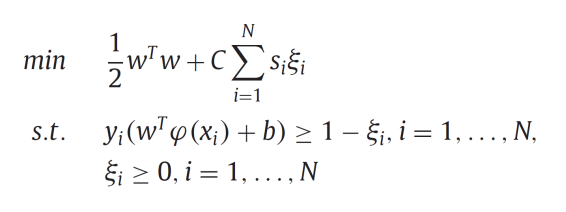
- s는 Soft margin SVM의 slack variable에 곱해져서 해당 데이터의 영향력을 낮추는 역할을 한다. 이 효과를 오직 negative class의 데이터에만 적용하여 imbalance dataset을 극복하는 것이 이 모델의 핵심이다.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from cvxopt import matrix as cvxopt_matrix
from cvxopt import solvers as cvxopt_solvers
data_ = pd.read_csv('D:/정석-한양대/4학년 2학기/응용데이터애널리틱스/creditcard_efsvm.csv', encoding = 'cp949', index_col = None)
columns_ = data_.columns
data_.head()
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | ... | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -1.004929 | -0.985978 | -0.038039 | 3.710061 | -6.631951 | 5.122103 | 4.371691 | -2.006868 | -0.278736 | -0.230873 | ... | 1.393406 | -0.381671 | 0.969719 | 0.019445 | 0.570923 | 0.333278 | 0.857373 | -0.075538 | 1402.95 | -1 |
| 1 | 1.154312 | 0.265462 | 0.384871 | 0.575007 | -0.217475 | -0.391520 | -0.081489 | 0.062789 | -0.260583 | -0.161677 | ... | -0.193213 | -0.557685 | 0.169492 | 0.186863 | 0.089252 | 0.093626 | -0.009633 | 0.019668 | 2.67 | -1 |
| 2 | 1.038370 | 0.127486 | 0.184456 | 1.109950 | 0.441699 | 0.945283 | -0.036715 | 0.350995 | 0.118950 | -0.243289 | ... | 0.102520 | 0.605089 | 0.023092 | -0.626463 | 0.479120 | -0.166937 | 0.081247 | 0.001192 | 1.18 | -1 |
| 3 | 1.287226 | -0.824683 | 1.346423 | -0.525628 | -1.833007 | -0.477715 | -1.224213 | 0.014774 | -0.257813 | 0.602162 | ... | -0.147633 | 0.057765 | 0.052105 | 0.428755 | -0.036979 | 1.112152 | -0.003678 | 0.031920 | 30.90 | -1 |
| 4 | -0.592060 | 0.785904 | 2.806517 | 2.935466 | -0.356682 | 1.127563 | -0.225130 | 0.514861 | -0.757541 | 0.523216 | ... | -0.105161 | -0.216887 | -0.190514 | -0.033156 | -0.001445 | 0.200179 | 0.109606 | 0.084341 | 18.96 | -1 |
5 rows × 30 columns
사용할 함수들
def Kernel_(x, y, params = 0, type_ = 'linear') :
if type_ == 'rbf' :
Kernel = np.exp(- (np.sum(x **2, axis = 1).reshape(-1,1) + np.sum(y **2, axis = 1).reshape(1,-1) - 2 * x @ y.T)* params)
return Kernel
elif type_ == 'linear' :
Kernel = np.dot(x, y.T)
return Kernel
def Minmax_(X) :
return (X - X.min(axis = 0)) / (X.max(axis= 0) - X.min(axis = 0)), X.max(axis =0) , X.min(axis =0)
def Standar_(X) :
return (X - X.mean(axis =0)) / X.std(axis = 0), X.mean(axis =0), X.std(axis = 0)
def Convolution(pred, real) :
pred = np.array(pred)
y = np.array(real)
TP = np.sum((pred == 1) & (y == 1))
FP = np.sum((pred == 1) & (y != 1))
FN = np.sum((pred != 1) & (y == 1))
TN = np.sum((pred != 1) & (y != 1))
return TP, FP, FN, TN
############## Accuracy is newly included!
def acc_precision_recall(X) :
TP,FP,FN,TN = X
return (TP + TN) / (TP + FP + FN + TN), TP / (TP + FP), TP / (TP + FN)
EFSVM 논리 구현
#Hyperparameters
C = 10
k = 7
m = 10
beta = 1/18
columnsX = data_.columns[:-1]
columnsY = data_.columns[-1]
X, y = data_[columnsX].copy(), data_[columnsY].copy()
Ypos = y[y == 1].index
Yneg = y[y == -1].index
Entropy_Yneg = pd.DataFrame()
distNeg = pd.DataFrame(distance.cdist(X, X.loc[Yneg], 'euclidean'), index = data_.index, columns=Yneg)
for i in Yneg :
numP = np.sum(y.loc[distNeg.loc[:, i].sort_values()[1:k+1].index] == 1)
numN = k - numP
probP = numP/k
probN = numN/k
H = entropy([probP, probN])
Entropy_Yneg.loc[i, 'numP'] = numP
Entropy_Yneg.loc[i, 'numN'] = numN
Entropy_Yneg.loc[i, 'probP'] = probP
Entropy_Yneg.loc[i, 'probN'] = probN
Entropy_Yneg.loc[i, 'H'] = H
Emax, Emin = Entropy_Yneg['H'].max(), Entropy_Yneg['H'].min()
FM = {}
for l in range(1, m+1):
thrUp = Emin + l/m * (Emax - Emin)
thrLow = Emin + (l-1) / m * (Emax - Emin)
if m == l :
Entropy_Yneg.loc[(Entropy_Yneg['H'] >= thrLow) & (Entropy_Yneg['H'] <= thrUp), 'subi'] = l
Entropy_Yneg.loc[(Entropy_Yneg['H'] >= thrLow) & (Entropy_Yneg['H'] <= thrUp), 'FM'] = 1 - beta * (l - 1)
else:
Entropy_Yneg.loc[(Entropy_Yneg['H'] >= thrLow) & (Entropy_Yneg['H'] < thrUp), 'subi'] = l
Entropy_Yneg.loc[(Entropy_Yneg['H'] >= thrLow) & (Entropy_Yneg['H'] < thrUp), 'FM'] = 1 - beta * (l - 1)
si = pd.DataFrame(index = data_.index)
si.loc[Ypos, 'si'] = 1
si.loc[Entropy_Yneg.index, 'si'] = Entropy_Yneg['FM'].values
si = np.array(si['si'])
Linear Kernel SVM에 적용
X = Standar_(np.array(data_[columns_[:-1]]))[0]
y = np.array(data_[columns_[-1]])* 1.
y = y.reshape(-1,1)
m,n = X.shape
#Kernel 관련 정의 numpy array 형식으로 생성
H = Kernel_(X, X) * 1.
H *= y@y.T
P = cvxopt_matrix(H)
q = cvxopt_matrix(-np.ones((m, 1)))
G = cvxopt_matrix(np.vstack((-np.eye(m),np.eye(m))))
h = cvxopt_matrix(np.hstack((np.zeros(m), np.ones(m) * C * si))) #alpha <= si * C
A = cvxopt_matrix(y.reshape(1, -1))
b = cvxopt_matrix(np.zeros(1))
#Run solver
sol = cvxopt_solvers.qp(P, q, G, h, A, b)
alphas = np.array(sol['x'])
w = ((y * alphas).T @ X).reshape(-1,1)
S = ((alphas.T > 1e-4) & (alphas.T < C * si -1e-4)).flatten()
b = y[S] - np.sum(Kernel_(X, X[S], type_ = 'linear')* y * alphas , axis = 0).reshape(-1,1)
print('Alphas = ',alphas[(alphas > 1e-4) & (alphas < C -1e-4)])
print('')
print('w = ', w.flatten())
print('')
print('b = ', np.mean(b))
print('')
print("support vector : ", np.array(range(m))[S])
pcost dcost gap pres dres
0: -1.5910e+03 -4.3471e+05 2e+06 1e+00 1e-11
1: -1.2615e+03 -1.9862e+05 4e+05 3e-01 6e-12
2: -9.4079e+02 -7.4281e+04 1e+05 8e-02 3e-12
3: -8.6022e+02 -5.1625e+04 9e+04 5e-02 2e-12
4: -7.9739e+02 -3.8295e+04 6e+04 3e-02 1e-12
5: -7.3697e+02 -2.6001e+04 4e+04 2e-02 1e-12
6: -6.8044e+02 -1.7693e+04 2e+04 8e-03 7e-13
7: -6.4836e+02 -1.1787e+04 1e+04 4e-03 6e-13
8: -6.4728e+02 -9.4078e+03 1e+04 2e-03 6e-13
9: -6.3148e+02 -7.2836e+03 7e+03 1e-03 6e-13
10: -6.8902e+02 -4.5431e+03 4e+03 5e-04 6e-13
11: -7.1881e+02 -3.8369e+03 3e+03 3e-04 6e-13
12: -7.3561e+02 -3.4946e+03 3e+03 2e-04 6e-13
13: -7.6325e+02 -2.8353e+03 2e+03 1e-04 6e-13
14: -7.7957e+02 -2.5450e+03 2e+03 1e-04 7e-13
15: -7.9487e+02 -2.4165e+03 2e+03 1e-04 7e-13
16: -7.8344e+02 -2.3828e+03 2e+03 9e-05 6e-13
17: -8.0844e+02 -1.8718e+03 1e+03 5e-05 6e-13
18: -8.1632e+02 -1.7548e+03 9e+02 4e-05 6e-13
19: -8.2726e+02 -1.6709e+03 8e+02 2e-05 7e-13
20: -8.3490e+02 -1.5903e+03 8e+02 2e-05 7e-13
21: -8.4449e+02 -1.5303e+03 7e+02 1e-05 7e-13
22: -8.6258e+02 -1.4448e+03 6e+02 7e-06 8e-13
23: -8.7233e+02 -1.4015e+03 5e+02 5e-06 7e-13
24: -8.7889e+02 -1.3590e+03 5e+02 4e-06 7e-13
25: -8.7057e+02 -1.3259e+03 5e+02 3e-06 8e-13
26: -8.8660e+02 -1.2207e+03 3e+02 1e-06 7e-13
27: -8.9131e+02 -1.2139e+03 3e+02 1e-06 8e-13
28: -8.9370e+02 -1.2018e+03 3e+02 1e-06 7e-13
29: -9.0529e+02 -1.1564e+03 3e+02 7e-07 8e-13
30: -9.0623e+02 -1.0818e+03 2e+02 3e-07 9e-13
31: -9.1486e+02 -9.7794e+02 6e+01 1e-07 1e-12
32: -9.1635e+02 -9.6975e+02 5e+01 5e-08 8e-13
33: -9.1835e+02 -9.4174e+02 2e+01 2e-08 8e-13
34: -9.1956e+02 -9.2971e+02 1e+01 2e-09 9e-13
35: -9.1979e+02 -9.2551e+02 6e+00 6e-10 9e-13
36: -9.1979e+02 -9.2549e+02 6e+00 6e-10 8e-13
37: -9.1983e+02 -9.2537e+02 6e+00 6e-10 8e-13
38: -9.1990e+02 -9.2423e+02 4e+00 4e-10 9e-13
39: -9.1996e+02 -9.2332e+02 3e+00 2e-10 8e-13
40: -9.2000e+02 -9.2276e+02 3e+00 1e-10 9e-13
41: -9.2008e+02 -9.2204e+02 2e+00 6e-11 9e-13
42: -9.2014e+02 -9.2165e+02 2e+00 3e-11 8e-13
43: -9.2017e+02 -9.2124e+02 1e+00 1e-11 8e-13
44: -9.2020e+02 -9.2091e+02 7e-01 1e-13 9e-13
45: -9.2023e+02 -9.2066e+02 4e-01 3e-13 8e-13
46: -9.2025e+02 -9.2048e+02 2e-01 2e-13 9e-13
47: -9.2028e+02 -9.2031e+02 3e-02 6e-14 1e-12
48: -9.2028e+02 -9.2030e+02 2e-02 1e-13 8e-13
49: -9.2028e+02 -9.2030e+02 2e-02 3e-13 9e-13
50: -9.2028e+02 -9.2030e+02 2e-02 2e-13 8e-13
51: -9.2028e+02 -9.2030e+02 2e-02 4e-13 9e-13
52: -9.2028e+02 -9.2030e+02 2e-02 1e-13 8e-13
53: -9.2028e+02 -9.2030e+02 2e-02 2e-14 8e-13
54: -9.2028e+02 -9.2029e+02 8e-03 6e-14 8e-13
55: -9.2028e+02 -9.2028e+02 3e-04 3e-13 1e-12
Optimal solution found.
Alphas = [0.01053436 0.01405414 0.035195 ... 0.01797992 0.13300897 0.0109052 ]
w = [ 0.02807682 0.14478151 -0.07408444 0.04216777 0.00483365 -0.04769694
-0.2711837 0.0403171 -0.04646144 -0.15687547 0.09686205 -0.2399348
-0.00321587 -0.27318425 -0.00449666 -0.18038055 -0.47529218 -0.09156313
0.02946959 -0.01851045 0.00668659 0.0117859 0.02966708 -0.00260104
0.0106047 0.00239085 0.00803754 0.01988052 0.14000624]
b = -0.7203327209106551
support vector : [ 0 1 2 ... 4991 4996 4999]
성능 확인
pred_sol = np.sign(np.sum(Kernel_(X, X ,type_ = 'linear')* y * alphas , axis = 0).reshape(-1,1) + b[0])
acc_precision_recall(Convolution(pred_sol,y))
(0.9908, 1.0, 0.816)