Jeongseok Oh

I am a student studying Data Science in Hanyang Univ.

2 minute read

개요

  • t-SNE는 고차원의 데이터셋을 저차원으로 mapping하기 위해 고안된 방법이다.
  • 기존의 SNE보다 robust한 결과를 보여주기 때문에 여전히 많이 사용되는 기술이다.
  • t-SNE에 대해 이해해보고 구현해보자.

t-SNE란?

  • t-SNE는 차원의 축소, 즉, 임베딩을 위한 알고리듬이다. Principle Component Analysis와 같이 훌륭한 차원 축소 기법들이 존재한다. 그러나 PCA는 선형적인 관계를 나타내기엔 용이하지만, 비선형적인 관계를 나타내기엔 부족했다.
  • t-SNE는 기존의 SNE 기법을 개선하여 만든 기법이다.
  • t-SNE는 고차원에서 nearest neighbor이었던 점들이 저차원에서도 여전히 nearest neighbor이길 바란다.

t-SNE의 원리

  • t-SNE는 원 공간(고차원)에서 임베딩 공간(저차원)으로 데이터의 변환을 꾀하는 기법이다. 이 과정에서 데이터 간 유사도가 변하지 않기를 바란다. 원 공간에서의 데이터 간 유사도를 p_ij, 임베딩 공간에서의 데이터 간 유사도를 q_ij로 정의한다.
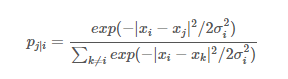
  • p_ij는 점 x_i에서 점 x_j로의 유사도인 p_j|i로 정의된다. 우선 기준이 되는 점 x_i에서 다른 모든 점들과의 거리(Euclidean Distance)인 |x_i - x_j|를 계산한다. 이 거리를 기반으로 x_i가 x_j를 이웃으로 뽑을 확률을 나타낼 수 있다. 위 거리를 σ^2으로 나누고 negative exponential을 취하여 가까울 수록 높은 확률을 갖는 exp(-|x_i - x_j|^2/2σ^2)의 꼴을 만든다. 그 후, 모든 점들과의 exp(-|x_i - x_j|^2/2σ^2)의 거리의 합으로 나누어 주면, 모두 더하면 1이 되는 확률이 된다. image-20220520005641410
  • σ는 x_i를 중심으로 하는 가우시안 분포의 분산이다.
  • 점들간의 유사도만을 보기 때문에 p_i i = 0 으로 둔다.
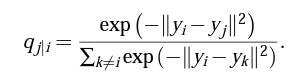
  • 임베딩 공간의 counterparts인 y_i와 y_j 또한 위의 방식처럼 계산할 수 있고, 우린 그것을 q_j|i라고 정의한다. 이때의 분산은 1/√2로 정의한다. q_j|i는 다음과 같다. image-20220520212639594
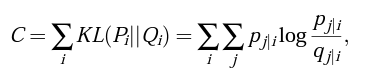
  • p_j|i와 q_j|i의 분포 차이가 최대한 작길 위하므로, 우린 KL Divergence를 사용하여 cost function을 세울 것이다.SNE의 cost function은 다음과 같으며, gradient descent method를 이용해서 문제를 풀 것이다. image-20220520212925326
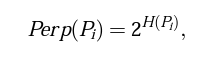
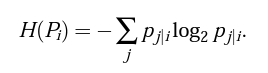
  • P_i를 유도하는 σ_i 에 의해 만들어지는 가우시안 분포는 σ_i가 커짐에 따라 커지는 엔트로피를 갖는다. SNE는 고정된 Perplexity를 갖는 P_i분포의 σ_i 값을 binary search를 통해 찾는다. Perplexity는 사용자에 의해 다음과 같이 정의된다. image-20220524194302666 image-20220524194535284
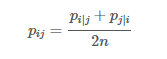
  • H(P)는 P분포의 엔트로피이다. Perp는 효과적인 Number of neighbors를 결정할 때 좋은 수단으로 해석 가능하다. 다만, SNE 알고리듬은 Perp값에 대해 robust하다. image-20220928202654957
  • 위와 같이 p_ij를 정의하면, x_i가 이상점(Outlier)일 시에 p_ij가 모든 j에 대하여 매우 작아져서 y_i로 하여금 cost function에의 영향이 매우 작아지는 것을 막을 수 있다. 이 방법은 모든 x_i에 대해서 모든 p_ij의 합이 1/2n보다 커지게끔 하여 모든 x_i가 cost function에 유의미한 영향을 주게끔 도와준다.
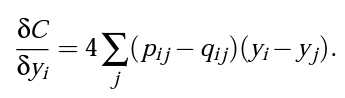
  • 마지막으로 아래와 같이 y_i에 대한 편미분을 통해 Cost function에 경사하강법을 진행하면 완성된다. image-20220928214837330
from sklearn.manifold import TSNE
from keras.datasets import mnist
import numpy as np
import pandas as pd
import seaborn as sns

#TSNE(n_components=2, perplexity=30.0, early_exaggeration=12.0,
#     learning_rate=200.0, n_iter=1000, n_iter_without_progress=300,
#     min_grad_norm=1e-07, metric='euclidean', init='random', verbose=0,
#     random_state=None, method='barnes_hut', angle=0.5)

(train_X, train_y), (test_X, test_y) = mnist.load_data()
x_train = train_X[:3000]
y_train = train_y[:3000]

x_mnist = np.reshape(x_train, [x_train.shape[0], x_train.shape[1]*x_train.shape[2]])
#tsne = TSNE(n_components=3)
#pred_y = tsne.fit_transform(x_mnist)


tsne = TSNE(n_components=2, verbose=1, random_state=123)
z = tsne.fit_transform(x_mnist)
df = pd.DataFrame()
df["y"] = y_train
df["component_1"] = z[:,0]
df["component_2"] = z[:,1]

sns.scatterplot(x="component_1", y="component_2", hue=df.y.tolist(),
                palette=sns.color_palette("hls", 10),
                data=df).set(title="MNIST data T-SNE projection")

[t-SNE] Computing 91 nearest neighbors...
[t-SNE] Indexed 3000 samples in 0.001s...
[t-SNE] Computed neighbors for 3000 samples in 0.216s...
[t-SNE] Computed conditional probabilities for sample 1000 / 3000
[t-SNE] Computed conditional probabilities for sample 2000 / 3000
[t-SNE] Computed conditional probabilities for sample 3000 / 3000
[t-SNE] Mean sigma: 480.474473
[t-SNE] KL divergence after 250 iterations with early exaggeration: 78.815842
[t-SNE] KL divergence after 1000 iterations: 1.262797





[Text(0.5, 1.0, 'MNIST data T-SNE projection')]

output_5_2 ​

You May Also Enjoy